这篇文章仅仅是简单的回顾一下决策树开始的一些经典算法，虽然较旧了，用的人少了，但是一些思想和算法，值得了解。下面主要介绍的算法有ID3、C4.5、CART、SLIQ、SPRINT，其中CART算法一笔带过吧，有些需要深究的部分，我也没有太理清，就把我现在理解的东西权当是记录一下把。

ID3

ID3(Iterative Dichotomiser 3)，迭代的二分法分离模型version 3，是根据信息增益来做的决策，所以如何定义信息增益是个主要的问题？首先来看一下信息熵的定义:
$H(S) = -\sum_{i=1}^{m} P(u_i)logP(u_i)$
其中$S$是样例的集合，$P(u_i)=\frac{|u_i|}{|S|}$，一般认为越有序的数据熵比较低，越乱序的则熵比较大，显然我们分类的目的就是有序，减少熵。最后的信息增益为:
$Gain(S,A)=Entropy(S) - \sum_{v \in Value(A)}\frac{|S_v|}{|S|}Entropy(S_v)$
遍历所有属性即可，这个算法优点就是简单，奥卡姆剃刀原理，缺点也较明显，抗噪音不行，无剪枝，最重要的是倾向于分类较多的节点分裂，这样其实没有太多意义，于是引入了C4.5算法。

C4.5

C4.5是对ID3的改进，因为ID3分裂出的树不是二叉树，而是有多少属性就有多少分叉，所以如果分叉过多，容易导致各个分支上的信息熵为0，但是这种明显不是我们想要的，所以这里提出了信息增益率的概念，公式为:
$GainRatio(A) = \frac{Gain(A)}{SplitInfo(A)}$
分母是训练集关于A的分布情况，显然，越多越大，最后的增益率就会下降。选择具有最大增益率的的属性作为分裂属性。
有点类似于后面的正则的概念，即SplitInfo(A)是正则项，如果分裂过多，这个值会弱化Gain(A)的影响。SplitInfo(A)的定义如下:
$$
SplitInfo_{A}(D) = -\sum_{j=1}^{v}\frac{|D_{j}|}{D}*\log_{2}(\frac{|D_{j}|}{D})
$$

CART

CART和C4.5类似，不过是使用gini算法计算收益，gini值越小，效果越好。接下来会讲一下gini算法的实现。

gini

基尼指数原来是是衡量贫富悬殊程度的标量。它的定义如下：我们首先收集社会上每一个人的总财富额，把它从少至大排序，计算它的累积函数（cumulative function），然后便可绘出图中的洛仑兹曲线（Lorenz curve）。图中横轴是人口比例的累积分布，竖轴是财富比例的累积分佈。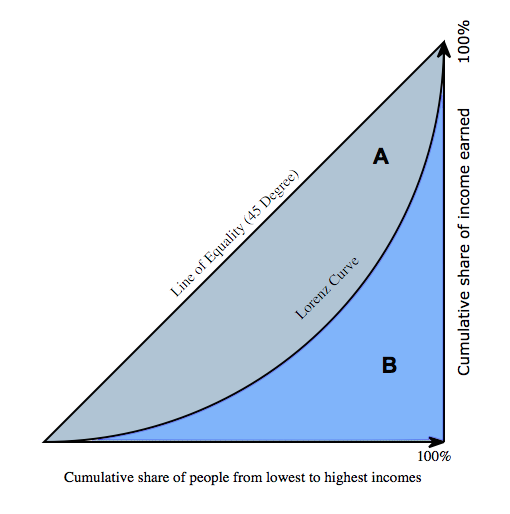
gini
$A$和$B$是图中两个面积，基尼系数为$\frac{A}{A+B}$
越不均匀，比如钱都集中在少数人手里，则$B$趋向于0，gini系数很大，python简单的实现如下:

1
2
3
4
5
6
7
8
9
import numpy as np
def gini_coef(wealths):
	cum_wealths = np.cumsum(sorted(np.append(wealths, 0)))
	sum_wealths = cum_wealths[-1]
	xarray = np.array(range(0, len(cum_wealths))) / np.float(len(cum_wealths)-1)
	yarray = cum_wealths / sum_wealths
	B = np.trapz(yarray, x=xarray)
	A = 0.5 - B
	return A / (A+B)

应用到具体分类的gini定义如下:
$gini(S)=1-\sum_{j=1}^{n}p_j^2$
$p_j$为类j出现的概率，如果集合分成$S_1$和$S_2$部分，则分割后的gini为
$gini_{split}(S)=\frac{n_1}{n}gini(S_1)+\frac{n_2}{n}gini(S_2)$
则$GAIN_{gini} = gini(S) - gini_{split}(S)$，越大收益越高。

gini系数收益的补充

上面提到的公式 $\sum_{j=1}^{n}p_j^2$很难和定义中的积分联系起来，及时联系的话$p_j$应该是越分散越好，和积分对应，分散说明积分面积大，gini系数越小，而这里明天是$p_j$越大约不分散好？怎么对应呢？
比如”p1=0.1, p2=0.1, p3=0.8”是比”p1=0.2, p2=0.2, p3=0.6”好的，可是按照积分来看，后面的明显积分面积更大？其实这里的误区是$p_j$不是横坐标对应的值，而应该是横坐标，即横坐标的范围，这里的积分即面积对应的是$p_j$*value，value取多少呢？这里就取得是$p_j$，这样就统一了。试想，如果国家有90%的人年收入超过1亿，那才好呢
插一下，国际惯例把0.2以下视为收入绝对平均，0.2-0.3视为收入比较平均；0.3-0.4视为收入相对合理；0.4-0.5视为收入差距较大，当基尼系数达到0.5以上时，则表示收入悬殊。而我国的gini系数可能超过了0.7?

如何收益大？

说到gini系数，其实有点相悖？gini系数中如果财产都在一个人手里，那岂不是显得很”纯”? 其实这种情况的确是比较符合理想分类的情形，因为99%的都是穷人，1%的才是富人，不过这样想就错了，因为负例太负了，负例产生的波动太大了，因为太大了，造成了整体的均值不回太低，所以其它99%的产生的mse也是比较大的，其实可以这么理解，一共100个样本，和就是1，如果均匀分布即大家都是同类人，这样才是分类的最佳情况。

SLIQ

super-vised learning in quest, 这个名字的确挺蛋疼的，应该叫一种可伸缩的分类器，这个算法有什么特点呢？如下总结
| BFS
| 直方图
| 属性表
| 类表
每个树节点都拥有了直方图(local)，属性表(global), 类表(global), 这样也才能使用BFS，特别每个树节点都拥有自己的直方图，可以统一扫一下属性表，然后整体更新树节点上的直方图，直方图如下表所示，假设只有两个分类C1,C2：
参数|描述

stats1 C1 C2
left 1 0
right 3 4

这个是最初的统计，其实实际在遍历中，可以用最大收益代替，并附上最大收益对应的attribute以及split_value，当然一般的算收益仍然是使用gini算法。

stats2 Gain Attr Value
stats 2.5 a1 6

每次扫描完毕，这当前所有的叶子节点(active nodes)上的直方图都会更新一次，决定了下一次的分裂, 如上面节点中的最佳分裂的属性是a1, $split_value=6$。优点很直观啊，全局一次排序。
补一下直方图、属性表、类表。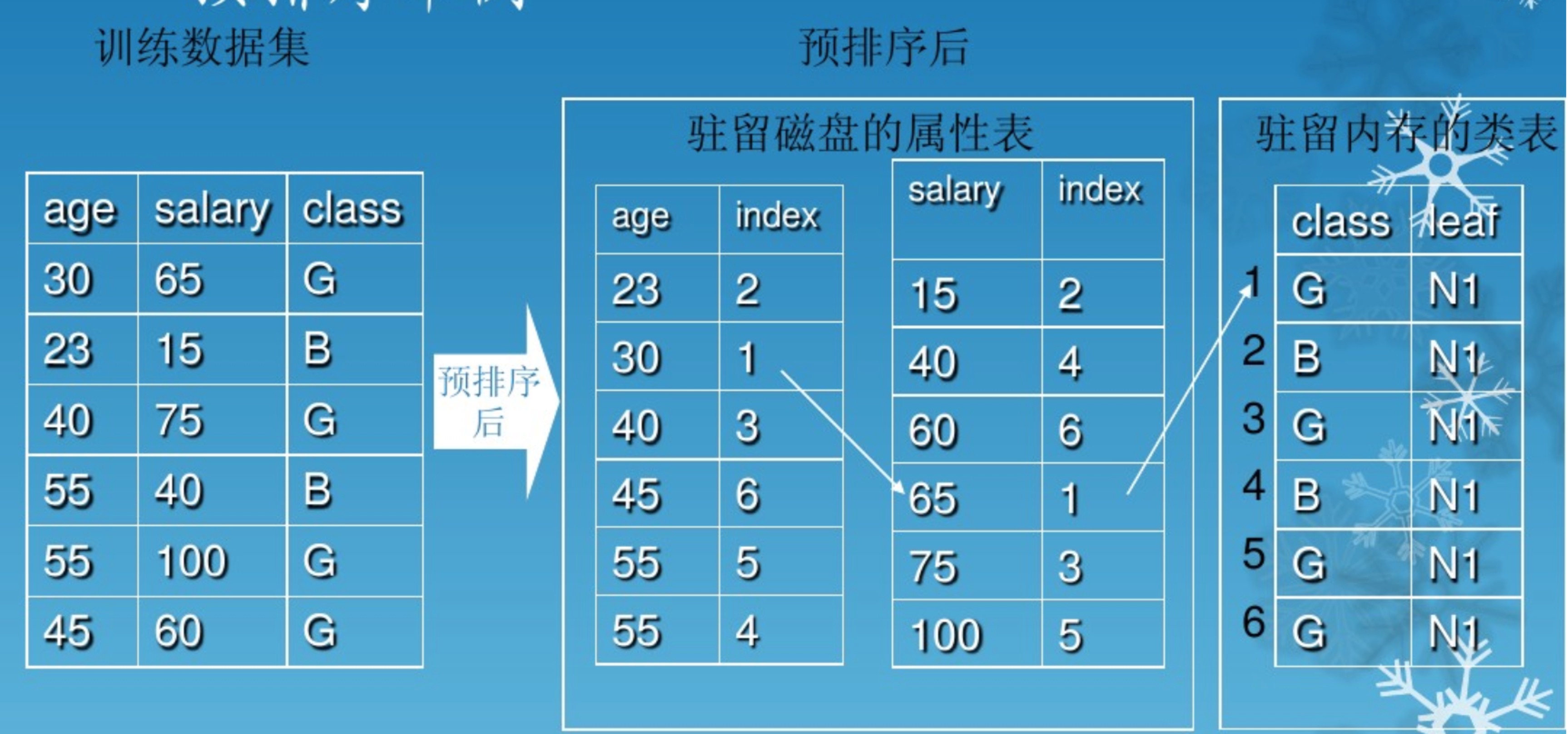
sliq
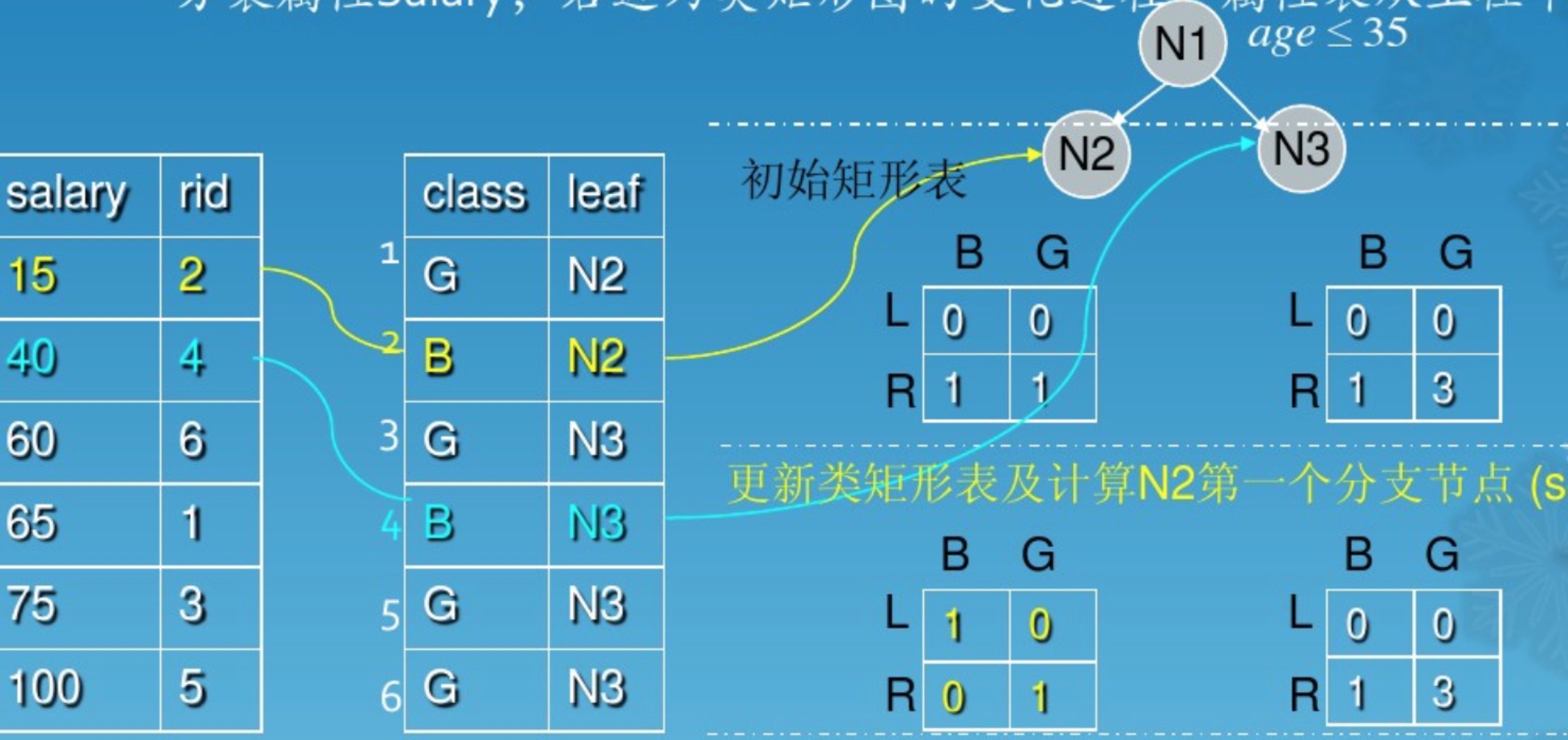
sliq2

SPRINT

scalable parallelizable induction(归纳) of decision trees, sprint算法，强调了并行，是在SLIQ的基础上更进一步, 将类图合并到每个属性表中，单独存入节点中，属性表随着节点的分裂也被分割，所以就不存在BFS了，而是深度优先遍历的方式，每个节点拥有自己单独的属性表(每个属性都需要一张(sorted))，可以单独分裂，这个可以加快并行，当然存储最佳分类的还是要使用直方图，这个算法的缺点就是每次分裂，需要设计到非分割属性表的元素分裂，需要通过rowid(hash?)对应上，分割相对复杂。

直方图如何对应xgboost?

分布式加权直方图算法,这是xgboost里带的，为了解决数据无法一次载入内存或者在分布式情况下算法，

可并行的近似直方图算法。树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost还提出了一种可并行的近似直方图算法，用于高效地生成候选的分割点。
直方图补充
微软新出的LightGBM算法也是用到了直方图，的确，这个直方图和SLIQ以及SPRINT的直方图并无区别，直方图直接在gbdt中使用，的确起到了比较好的效果，不过相对于level-wise，每个节点都需要维护自己的数据，各个feature上sort的数据，比较麻烦，不过这样的好处就是deep-wise，脱离了深度的限制，另外，LightGBM中使用了bin value作为划分根据，即将feature value专为bin value，一般一个字节，即最多256种划分，这样的好处就是存储压力变小，另外不必扫描所有的feature value，只需扫描256次即可，还有一个就是数据分割时较快速，因为内存占用少，共享索引表，直接划分，还有做差的方式，即处理好一个分裂节点，另一个节点直接通过与父节点作差即可得到，速度又得到了提高。

剪枝算法

分为预剪枝和后剪枝

  • 预剪枝
    1) 树高度
    2) 叶子节点的纯度以及叶子节点总数
  • 后剪枝
    只说一种吧，用验证集自底向上看节点的拟合率