背景

短文本question-answer匹配度识别问题，论文(Learning to Rank Short Text Pairs with Convolutional Deep Neural Networks.pdf), github实现。github的作者基本上实现了文章里的算法，计算的精度也差不多，不过使用theano实现的，我准备使用tensorflow实现，并解决大规模预料训练太慢的问题。当然本文要开始从分析git的实现开始讲起，会穿插theano的一些语法，实现等，我自己也是从零学起的，且当给自己留个笔记吧。

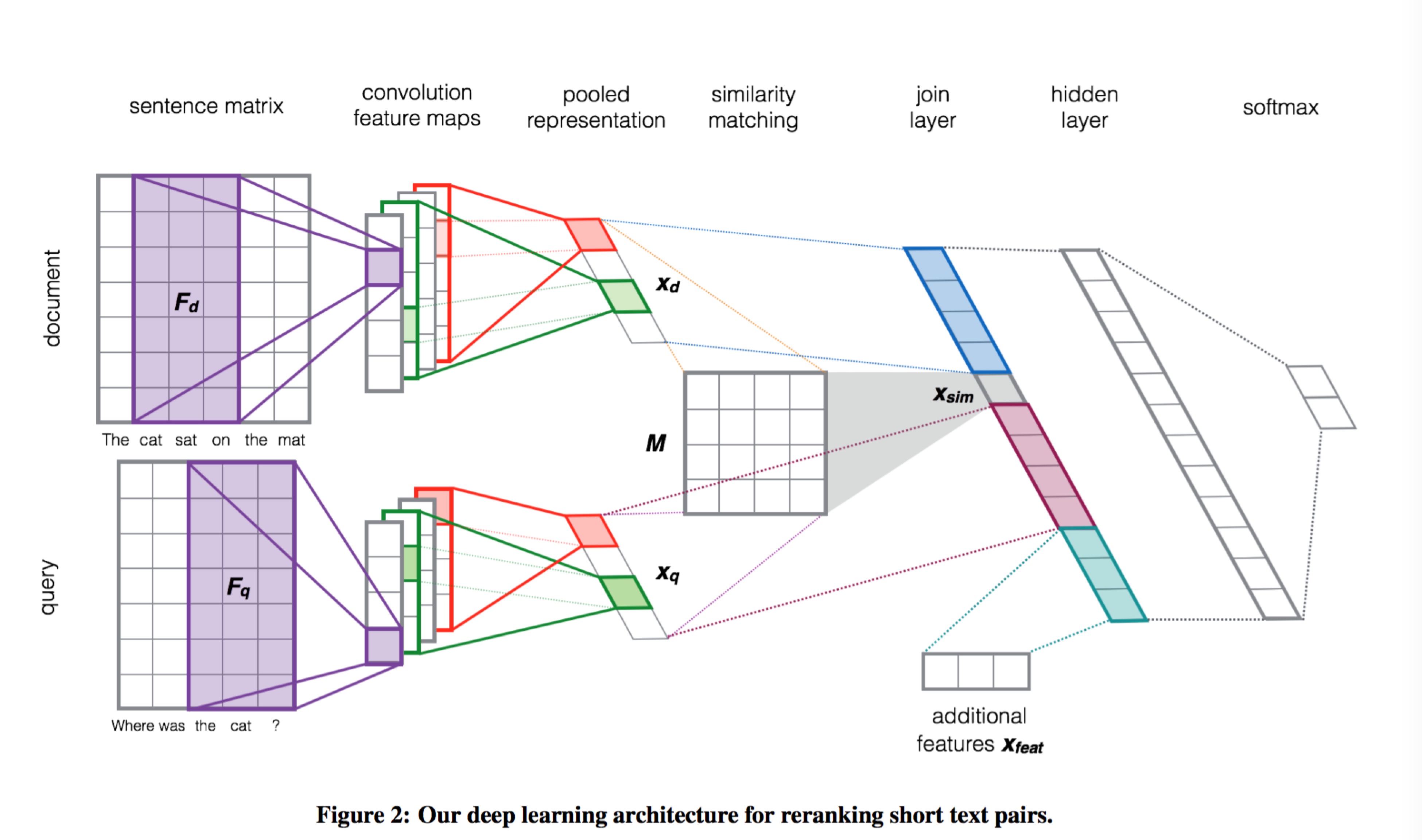
架构？

不能不提到的论文中经典的架构图。

网络用文字梳理的结果如下:

  1. question answer并行处理成词向量
  2. 词向量与卷积核做运算得到n个len(q or a)维的向量
  3. 对2中得到的向量做Activation和Pooling处理，得到1维数组，大小为n
  4. 问题和答案抽出的1维数组分别与相似度矩阵M做乘积预算，得到相似度，即 $A*M*Q=sim$
  5. 计算answer和question中的相同部分F，将A,sim,Q,F拼接成新的向量
  6. 将5中得到的向量做线性变化，即 $\alpha(W*X+b)$
  7. 最后使用Softmax对6中得到的linear之后的向量做分类

使用theano的实现

作者的实现有一些改动，如第5步骤中计算得到的交叉部分F，这部分可以是交叉词的词向量，也可以是交叉词的idf，比重等，显然idf和比重更容易让人信服，不过这个值不好处理，作者并没有用，而是直接使用的交叉词的词向量拼到question和answer的词向量中，即将这部分直接放到开头做了。

数据预处理(embedding)

这部分主要是将question-answer对分词(英文就是空格直接分词), 然后根据word2vec，将问题和答案分解成word2vec的词向量，并收集全集词表，word2vec缺失的词使用默认值填充。难点在于训练集合的选取，这是有监督的学习，对于中文的海量语法来说，需要的训练集合的规模也是非常大的。

Load

主要load的数据有train, dev, test三类，train是训练参数使用，dev是验证参数，test是实测使用，其实dev和test可以归为一类，每类数据分为question, answer, overlap。

词向量转化

LookupTableFast将question, answer, overlap转化为词向量。这里会讲pad部分(即卷积的宽度补上)，最后输出的是 [batch_size, 1, 2 * (q_size + q_filter_widths - 1), ndim], ndim是词向量的宽度(word2vec生成的词向量的size)，后面ndim的长度会拓展为

1
2
# sentence长度 + 交叉长度
ndim = vocab_emb.shape[1] + vocab_emb_overlap.shape[1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class LookupTableFastStatic(Layer):
	def __init__(self, W=None, pad=None):
		super(LookupTableFastStatic, self).__init__()
		self.pad = pad
		self.W = theano.shared(value=W, name='W_emb', borrow=True)
		def output_func(self, input):
			out = self.W[input.flatten()].reshape((input.shape[0], 1, input.shape[1], self.W.shape[1]))
			if self.pad:
				pad_matrix = T.zeros((out.shape[0], out.shape[1], self.pad, out.shape[3]))
	  			out = T.concatenate([pad_matrix, out, pad_matrix], axis=2)
	  		return out
	  def __repr__(self):
		  return "{}: {}".format(self.__class__.__name__, self.W.shape.eval())

卷积

定义Conv2dLayer来做卷积类使用，卷积的初始化如下

1
2
3
4
5
def __init__(self, rng, filter_shape, input_shape=None, W=None):
# @rng: 初始化种子
# @filter_shape: 卷积核的样式，filter_shape = (nkernels, num_input_channels, filter_width, ndim), nkernels = 100, num_input_channels = 1, 可见与question长度无关。
# @input_shape: 同上一层词向量层的输出
# @self.W 也和filter_shape具有相同的shape，随机化一些数字

卷积使用库函数，调用如下

1
2
3
4
def output_func(self, input):
	return conv.conv2d(input, self.W, border_mode='valid',
			filter_shape=self.filter_shape,
			image_shape=self.input_shape)

看看conv2d函数的返回, 看到output的是 [batch_size, filter_size, sentence_size, ndim]

1
2
3
4
5
6
7
8
9
10
Parameters:	
input (dmatrix of dtensor3) – Symbolic variable for images to be filtered.
filters (dmatrix of dtensor3) – Symbolic variable containing filter values.
border_mode ({'valid', 'full'}) – See scipy.signal.convolve2d.
subsample – Factor by which to subsample output.
image_shape (tuple of length 2 or 3) – ([number images,] image height, image width).
filter_shape (tuple of length 2 or 3) – ([number filters,] filter height, filter width).
kwargs – See theano.tensor.nnet.conv.conv2d.
Returns:	
Tensor of filtered images, with shape ([number images,] [number filters,] image height, image width)

何为卷积？如何卷积?
卷积为分时加权，在词向量上表现为分段计算作为权重，粒度更细了，input_shape细化为单个qa，即为如下格式(加上filter_width)。引用某乎上对卷积的解释:

cnn的核心在于卷积核，其实关于卷积核还有另一个名字叫做滤波器，从信号处理的角度而言，滤波器是对信号做频率筛选，这里主要是空间-频率的转换，cnn的训练就是找到最好的滤波器使得滤波后的信号更容易分类，还可以从模版匹配的角度看卷积，每个卷积核都可以看成一个特征模版，训练就是为了找到最适合分类的特征模板。

卷积核最后是作为最终的feature，每个卷积核作为一个特征，与question、answer等都无关了，所以卷积核的特征采集是非常重要的。

$$
S =
\begin{vmatrix}
| & | & … & | & | \\
filter & w_1 & … & w_{|s|} & filter \\
| & | & … & | & | \\
\end{vmatrix}
$$
$S.shape = [ndim, 2 \cdot (filter - 1) + len(s)]$
卷积核为[dim, m]维度，卷积公式如下:
$c_i=S \cdot f=S^T_{[i:i+m-1]} \cdot f=\sum_{k=i}^{i+m-1} s_kf_k$
注意是S的转置矩阵与f的相乘, 最后得到的是$[2 \cdot filter + |s|]$的宽度数组，即为卷积结果。增加filter_width是为了让S的每个word享受到相同的卷积效果。

Activation (tanh)

使用nn_layers.NonLinearityLayer作为主类，初始化以及output函数:

1
2
3
4
NonLinearityLayer(b_size=filter_shape[0], activation=activation)
def output_func(self, input):
	return self.activation(input + self.b.dimshuffle('x', 0, 'x', 'x'))

dimshuffle是将b拓展到4维，正好与卷积的output匹配相加。这里有一个问题，卷积出的第四维度是ndim，和公式算的$c_i$没有该维度，该维度上直接相加了。

Pooling

1
2
3
# 在第二维度上，即image height，也就是sentence
def max_pooling(input):
  return T.max(input, axis=2)

PairwiseNoFeatsLayer

这个是将q和a经过上面一系列的层产生的结果(最后是经过Pooling处理得到的[batch_size, n])做乘积，求q和a的相似性sim，最后将q,a,sim拼接。

1
2
3
4
5
6
7
8
# 注意这里的参数W矩阵是(n * n)的
def output_func(self, input):
	# P(Y|X) = softmax(W.X + b)
	q, a = input[0], input[1]
	# dot = T.batched_dot(q, T.batched_dot(a, self.W))
	dot = T.batched_dot(q, T.dot(a, self.W.T))
	out = T.concatenate([dot.dimshuffle(0, 'x'), q, a], axis=1)
	return out

out的长度为q_logistic_n_in + a_logistic_n_in + 1

LinearLayer

线性变换，这里的输入是长度为q_logistic_n_in + a_logistic_n_in + 1的特征数组，需要经过线性变化，LinearLayer

1
2
3
# W是(q_logistic_n_in + a_logistic_n_in + 1) * (q_logistic_n_in + a_logistic_n_in + 1)
def output_func(self, input):
    return self.activation(T.dot(input, self.W) + self.b)

LogisticRegression

最后一步，上面的输入仍然是q_logistic_n_in + a_logistic_n_in + 1, 使用softmax输出求解，

1
2
3
4
5
def output_func(self, input):
	# P(Y|X) = softmax(W.X + b)
	self.p_y_given_x = T.nnet.softmax(self._dot(input, self.W) + self.b)
	self.y_pred = T.argmax(self.p_y_given_x, axis=1)
	return self.y_pred

注意T.argmax是获取下标，所以这里的输出是直接分类(本问题中是0,1), p_y_given_x是给的具体的概率值。

训练网络

前面的整个网络已经布局完毕，是计算loss的时候了，cost=negative_log_likelihood(y)=-T.mean(T.log(self.p_y_given_x)[T.arange(y.shape[0]), y]), 使用adadelta训练参数，这个cost如何理解呢？找到了解释，我自己是没有跑通，囧。

1
2
3
4
5
6
7
8
9
10
11
# y.shape[0] is (symbolically) the number of rows in y, i.e.,
# number of examples (call it n) in the minibatch
# T.arange(y.shape[0]) is a symbolic vector which will contain
# [0,1,2,... n-1] T.log(self.p_y_given_x) is a matrix of
# Log-Probabilities (call it LP) with one row per example and
# one column per class LP[T.arange(y.shape[0]),y] is a vector
# v containing [LP[0,y[0]], LP[1,y[1]], LP[2,y[2]], ...,
# LP[n-1,y[n-1]]] and T.mean(LP[T.arange(y.shape[0]),y]) is
# the mean (across minibatch examples) of the elements in v,
# i.e., the mean log-likelihood across the minibatch.
return -T.mean(T.log(self.p_y_given_x)[T.arange(y.shape[0]), y])

如何更新参数呢？

1
updates = sgd_trainer.get_adadelta_updates(cost, params, rho=0.95, eps=1e-6, max_norm=max_norm, word_vec_name='W_emb')

作者实现的adadelta算法如下所示, 加上了我自己的理解和注释，我感觉这块的实现有些问题，因为adadelta是前t次的迭代，而这里的和显然是从开始到结束，有点像adagrad。后面贴的链接是几种求参迭代的方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
def get_adadelta_updates(cost, params, rho=0.95, eps=1e-6, max_norm=9, word_vec_name='W_emb'):
	print "Generating adadelta updates"
	updates = OrderedDict({})
	exp_sqr_grads = OrderedDict({})
	exp_sqr_ups = OrderedDict({})
	gparams = []
	# 这里设置了三个变量, for every param：
	# exp_sqr_grads init zeros
	# exp_sqr_ups zeros
	# gparams [] list append gp(grad)
	for param in params:
		exp_sqr_grads[param] = build_shared_zeros(param.shape.eval(), name="exp_grad_%s" % param.name)
		print 'cost ', cost
		print 'param.shape.eval', param.shape.eval()
		gp = T.grad(cost, param)
		print 'gp', gp
		exp_sqr_ups[param] = build_shared_zeros(param.shape.eval(), name="exp_grad_%s" % param.name)
		print 'exp_sqr_ups', exp_sqr_ups[param].shape
		gparams.append(gp)
		print param, gp
	#真正的计算, for every param
	# exp_sg 之前的 sum(sqr(gp) 1...t-1) for now param
	# exp_su 之前的 sum(step 1...t-1) for now param
	# up_exp_sg = rho * exp_sg + (1 - rho) * T.sqr(gp); 加上现在的gp平方
	# updates[exp_sg] = up_exp_sg 换上
	# step =  -(T.sqrt(exp_su + eps) / T.sqrt(up_exp_sg + eps)) * gp,该次更新的param step,
	  注意这里分母的gp是1..t，而分子的sum(step)是 1...t-1
	#updates[exp_su] = rho * exp_su + (1 - rho) * T.sqr(step); 更新本次
	#stepped_param = param + step;最后目标
	for param, gp in zip(params, gparams):
		exp_sg = exp_sqr_grads[param]
		exp_su = exp_sqr_ups[param]
	 	up_exp_sg = rho * exp_sg + (1 - rho) * T.sqr(gp)
	 	updates[exp_sg] = up_exp_sg
		step =  -(T.sqrt(exp_su + eps) / T.sqrt(up_exp_sg + eps)) * gp
	 	updates[exp_su] = rho * exp_su + (1 - rho) * T.sqr(step)
	 	stepped_param = param + step
		# if (param.get_value(borrow=True).ndim == 2) and (param.name != word_vec_name):
	 	if max_norm and param.name != word_vec_name:
			col_norms = T.sqrt(T.sum(T.sqr(stepped_param), axis=0))
			desired_norms = T.clip(col_norms, 0, T.sqrt(max_norm))
			scale = desired_norms / (1e-7 + col_norms)
			updates[param] = stepped_param * scale
		else:
			updates[param] = stepped_param
	return updates

参考资料:
http://blog.csdn.net/luo123n/article/details/48239963
http://sebastianruder.com/optimizing-gradient-descent/index.html#gradientdescentvariants
http://www.cnblogs.com/neopenx/p/4768388.html
http://deeplearning.net/tutorial/code/lstm.py